分治法 —— 平面上最小点对

平面上最小点对

给定平面上 n 个点，找出其中的一对点的距离，使得在这 n 个点的所有点对中，该距离为所有点对中最小的。
又是分治，（现在做梦tm都是分治了）,都是自己作的

还是书归正传，一样的，将所有的但分为两个部分，同样的左右部分，同样分别求其两部分的最小值，最后再合并。但是合并的情况比较特殊，为了明晰思路，借鉴大佬的证明：

假设dis为左右两部分中的最小距离：

最近距离不一定存在于两个集合中，可能一个点在集合 A，一个点在集合 B，而这两点间距离小于 dis。其中如何合并是关键。根据递归的方法可以计算出划分的两个子集中所有点对的最小距离 disleft,disright，再比较两者取最小值，即 dis=min(dis_{left},dis_{right}) 。那么一个点在集合 A，一个在集合 B 中的情况，可以针对此情况，用之前分解的标准值，即按照 x 坐标(或者 y )从小到大排序后的中间点的 x 坐标作为 mid。划分一个 [mid-dis,mid+dis] 区域，如果存在最小距离点对，必定存在这个区域中。

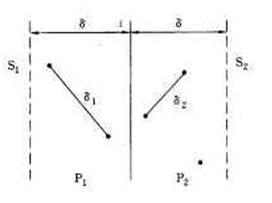
之后只需要根据左边区域 [mid-dis,mid] 的点来遍历右边区[mid,mid+dis] 的点，即可找到是否存在小于 dis 距离的点对。
但是存在一个最坏情况，即通过左右两个区域计算得到的 dis 距离来划分的第三区域可能包含集合所有的点，这时候进行遍历查找，时间复杂度仍然为O(n^2)。因此需要对此进行深一步的考虑。
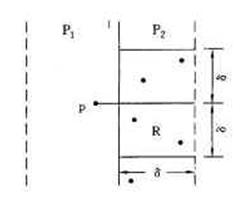1985年 Preparata 和 Shamos 在给出该问题的一个分治算法并且还具体分析了在 [mid-dis,mid+dis] 区域中出现的情况，若 (p,q) 是 Q 的最近点对，p 在带域左半部分，则 q 点必在下图所示的 δ∗2δ 长方形上，而在该长方形上，最多只能由右边点集的6个点。每个点对之间的距离不小于δ。
此结论很好证明，通过在 δ∗2δ 上以 \frac{2\delta}{3} 划成 6 个小长方形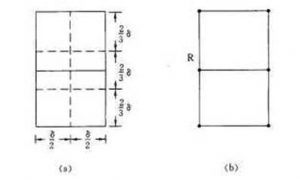
用反证法来证明，假设存在大于6个点，则必有一个或多个小长方形存在两个及以上点，而小长方形的最长距离是为对角线长度，为: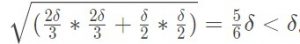
最长距离都小于δ，与之前的条件不符合，故最多有6个点。

代码如下

#include <iostream>
#include <algorithm>

using namespace std;


typedef struct Point         //点结构体
{
    double x;
    double y;
}*point,Point_xy;

Point_xy p[200010];
Point_xy temp[200010];
double dis = INFINITY;


double distance_points(Point_xy a, Point_xy b)        //计算两点之间距离
{
    double power_x = pow((a.x - b.x), 2.0);
    double power_y = pow((a.y - b.y), 2.0);
    return sqrt(power_x + power_y);
}

bool cmpx(const Point_xy& a, const Point_xy& b)     //将x从小到大排序
{
    return a.x < b.x;
}

bool cmpy(const Point_xy& a, const Point_xy& b)     //将y从小到大排序
{
    return a.y < b.y;
}

double rec(int left, int right)
{
    if (left == right)         //只有1个点，返回无穷大
        return dis;
    if (left + 1 == right)
        return distance_points(p[left],p[right]);    //只有2个点，只能两点之间距离
    int mid = (left + right) / 2;
    double dis1 = rec(left, mid);             //左集合的最小点对
    double dis2 = rec(mid + 1, right);        //右集合的最小点对
    dis = min(dis1, dis2);                   //左右两个集合中最小者

    int i, j, k = 0;
    for (i = left; i <= right; i++)           //距离分割线小于dis的点记录下来
    {
        if (fabs(p[i].x - p[mid].x) <= dis)
            temp[k++] = p[i];
    }
    sort(temp, temp + k, cmpy);             //关于y的大小对所记录的点排序
    for (i = 0; i < k; i++)
    {
        for (j = i + 1; j < k; j++)
        {
            if ((temp[j].y - temp[i].y) <= dis)
                dis = min(dis, distance_points(temp[i], temp[j]));  //当y方向上的距离也小于dis时才符合条件
            else break;
        }
    }
    return dis;
}


int main()
{
    int n; cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> p[i].x >> p[i].y;
    }
    sort(p, p + n, cmpx);
    double ans = rec(0, n - 1);
    cout << ans << endl;
    return 0;
}