图 —— 拓扑排序

图的“高端操作”—— 拓扑排序。（一直在还债，后悔数据结构没有好好学。。。）

拓扑排序

所谓拓扑排序，就是将图的节点按照一定的顺序排序（废话）。而排序的顺序是按照父子节点优先级排序，一个简单的例子

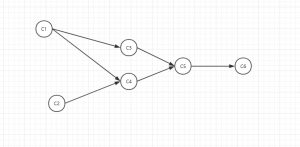
C1–C6代表不同的6门课程，而课程之间的优先级与关系如图所示：如上C3之前必须上C1，上C5之前必须上C3，C4……

进行拓扑排序有一个先决条件：图必须为有向无关图（无环有向图）

核心算法：

topo_sort()
{
    for (int counter=0; counter<=Graph.vexNum; counter++)
    {
        vextex v=findNewVertexOfIndegreeZero();
        if (v=NOT_A_VERTEX)
            throw CircleFoundException();
        v.topNum=counter;

        for each Vertex w adjecent to vex
            w.indegree--;
    }
}

代码实现：

//图——拓扑排序

#include <iostream>
#include <stack>
#include <algorithm>
#include <memory.h>

#define MAXNUM 100

using namespace std;

stack<int> s;
int indegree[MAXNUM];
int count_it = 0;
typedef struct Node
{
    int adjvex;
    Node* next;
}adj;

adj ad[MAXNUM];

void Create(adj a[], int vNum, int eNum)
{
    int i;
    adj* p;
    for (i = 1; i <= vNum; i++)
    {
        a[i].adjvex = i;
        a[i].next = NULL;
    }
    for (i = 1; i <= eNum; i++)
    {
        cout << "输入第" << i << "条边的起点与终点：";
        int start, end;
        cin >> start >> end;
        p = new adj;
        p->adjvex = end;
        p->next = a[start].next;
        a[start].next = p;
    }
}

void topo_sort(adj a[], int vNum)
{
    int i;
    adj* p;
    memset(indegree, 0, sizeof(indegree));
    for (i = 1; i <= vNum; i++)
    {
        p = a[i].next;
        while (p != NULL)
        {
            indegree[p->adjvex]++;
            p = p->next;
        }
    }
    for (i = 1; i <= vNum; i++)
    {
        if (indegree[i] == 0)
            s.push(i);
    }

    while (s.size() != 0)
    {
        i = s.top();
        s.pop();
        cout << i << ' ';
        count_it++;
        for (p = a[i].next; p != NULL; p = p->next)
        {
            int k = p->adjvex;
            indegree[k]--;
            if (indegree[k] == 0)
                s.push(k);
        }
    }
    cout << endl;
    if (count_it < vNum)
    {
        cout << "有回路，拓扑排序失败！" << endl;
    }
}

int main()
{
    int vNum, eNum;
    cout << "输入点数：";
    cin >> vNum;
    cout << "输入边数：";
    cin >> eNum;
    Create(ad, vNum, eNum);
    cout << "拓扑排序结果为：" << endl;
    topo_sort(ad, vNum);
    system("pause");
    return 0;
}

以上述图为例：