图——环

来交作业了。。。
这几天都没有更东西，一边是有作业难，一边是编译器经常崩溃（就不能是懒吗？） 有一说一，之前真没有怎么研究过类问题（就是数据结构没学好）

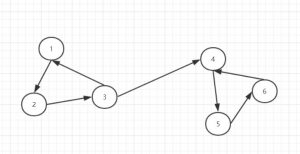
图的环的问题需要分情况，分有向图与无向图。

1.将所有节点涂白，表示节点未被访问；
2.从其中某一节点开始深度优先遍历，将访问过的节点涂灰；
3.如果其后裔节点均被访问过，则将节点涂黑，表示不再访问；
4.若某个已被涂灰的节点又被访问到，则有环的产生，并计数；
5.进行特判，自己指向自己不能算作环。

核心算法:

dfs_circle(graph g, int i)
{
    count=0;
    color[i]==Gray;
    for (j=1; j<=g->vNum; j++)
    {
        if(exist(Edge))             //边存在
        {
        if (color[i]==Gray)         //该节点被已涂灰
            if(vi!=vj)              //非自己指向自己的边
                count++;            //环数加一
        else if (color[i]==White)   
            dfs_circle(g,j);        //未被访问，继续dfs
        }
    }
    color[i]=Black;                 //后裔节点被访问，涂黑
}

实现代码：

//有向图 —— 环

#include <iostream>

#define MAXNUM 100
#define White 0
#define Gray -1
#define Black 1

using namespace std;

int color[MAXNUM];
int pre[MAXNUM];
int sum_circle = 0;
typedef struct graph
{
    int e[MAXNUM][MAXNUM];
    int vNum;
    int eNum;
}graph;                                      //用邻接矩阵存储图

void Create_Graph(graph* g)                  //创建图
{
    cout << "输入顶点个数：" << endl;
    cin >> g->vNum;
    cout << "输入边的个数：" << endl;
    cin >> g->eNum;
    int i, j, k;
    for (i = 1; i <= g->vNum; i++)
        for (j = 1; j <= g->vNum; j++)
            g->e[i][j] == 0;
    cout << "输入边的起点与终点：" << endl;
    for (k = 1; k <= g->eNum; k++)
    {
        cin >> i >> j;
        g->e[i][j] = 1;
    }
}

void dfs_circle(graph* g, int i)
{
    color[i] = Gray;      //该节点被访问
    for (int j = 1; j <= g->vNum; j++)
    {
        if (g->e[i][j] != 0)
        {
            if (color[j] == Gray)               //有环
            {
                if (i != j) sum_circle++;   //以防独自成环即a->a,环数加一 
            }
            else if (color[j] == White)
                dfs_circle(g, j);
        }
    }
    color[i] = Black;                      //子节点已访问完，该节点涂黑，不再访问
}

void DFS(graph* g)
{
    int i;
    for (i = 1; i <= g->vNum; i++)
    {
        color[i] = White;               //将所有节点设置为未被访问
    }
    for (i = 1; i <= g->vNum; i++)
    {
        if (color[i] == White)          //若节点未被访问，从该节点开始dfs_circle
            dfs_circle(g, i);
    }
}

int main()
{
    graph* g;
    g = new graph();
    Create_Graph(g);
    DFS(g);

    if (sum_circle==0) cout << "无环，是有向无关图" << endl;
    else 
    {
        cout << "有环" << endl;
        cout << "环的个数为：" << sum_circle << endl;
    }
    return 0;
}

—

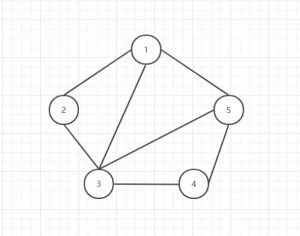
### 无向图

无向图这里要介绍一种比较有意思的图的存储结构 —— 链式前向星

typedef struct Node
{
    int to, next;     //to表示该边指向的终点， next表示与这条边起点相同的上一条边的编号
}Edge;               //边集

Edge e[MAXNUM];
int head[MAXNUM];
void add_edge(int start, int end)
{
    e[cnt].to = end;               //该条边指向的终点
    e[cnt].next = head[start];     //以u为起点上一条边的编号，也就是与这个边起点相同的上一条边的编号
    head[start] = cnt++;           //更新以u为起点的边的编号
}

先来说以下什么是前向星：

前向星是一种特殊的边集数组,我们把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序,并记录下以某个点为起点的所有边在数组中的起始位置和存储长度,那么前向星就构造好了.

链式前向星则在建立的时候就将顺序排好，将最大的边（起点相同，终点最大）的边放在第一个，依次降序排列。遍历时就进行逆向遍历。

1.从某一节点开始dfs，将访问过的节点涂灰

2.逆向遍历，并记录边的终点
3.若节点是白色，则继续dfs
4.若节点是灰色的，则开始找环

核心算法:

dfs_num_of_circle(int start, int find)
{
    int sum=0;
    visit[start] = Gray;                   //从start节点开始遍历，将start节点涂灰
    for (int i = head[start]; i; i = e[i].next)    //逆向遍历
    {
        int flag = e[i].to;               //flag记录边i所指向的终点
        if (flag == find) continue;      //无向图，a->b与b->a相同
        if (visit[flag] == White )        //若没有访问过就标记前一个元素
        {
            dfs_num_of_circle(flag, start);
        }
        else if (visit[flag] == Gray)       //若已经被访问过，开始找环及路径
            sum++;                          //环的个数++
    }
    visit[start] = Black;     //后裔节点遍历完，涂黑，不再访问
}

实现代码：

//无向图 —— 环

#include <iostream>

#define MAXNUM 100
#define White 0
#define Gray 1
#define Black 2

using namespace std;
int head[MAXNUM];
int cnt = 0, sum = 0;
int visit[MAXNUM];
int pre[MAXNUM];
typedef struct Node
{
    int to, next;     //to表示该边指向的终点， next表示与这条边起点相同的上一条边的编号
}Edge;               //边集

Edge e[MAXNUM];

void add_edge(int start, int end)
{
    e[cnt].to = end;               //该条边指向的终点
    e[cnt].next = head[start];     //以u为起点上一条边的编号，也就是与这个边起点相同的上一条边的编号
    head[start] = cnt++;           //更新以u为起点的边的编号
}

void dfs_num_of_circle(int start, int find)
{
    visit[start] = Gray;                   //从start节点开始遍历，将start节点涂灰
    for (int i = head[start]; i; i = e[i].next)
    {
        int flag = e[i].to;               //flag记录边i所指向的终点
        if (flag == find) continue;      //无向图，则a->b与b->a相同
        if (visit[flag] == White )        //若没有访问过就标记前一个元素
        {
            pre[flag] = start;
            dfs_num_of_circle(flag, start);
        }
        else if (visit[flag] == Gray)       //若已经被访问过，开始找环及路径
        {
            cout << "输出环的路径：" << endl;
            int temp = start;

            while (temp != flag)
            {
                cout << temp << " ";
                temp = pre[temp];
            }
            cout << flag << endl;
            sum++;                    //环的个数++
        }
    }
    visit[start] = Black;     //涂黑，不再访问
}



int main()
{
    int n, m, start, end;
    cout << "输入点的个数：" << endl;
    cin >> n;
    cout << "输入边的个数：" << endl;
    cin >> m;

    for (int i = 1; i <= m; i++)            //初始化边
    {
        cout << "输入第" << i << "条边的起点: ";
        cin >> start;
        cout << "输入第" << i << "条边的终点: ";
        cin >> end;
        add_edge(start, end);
        add_edge(end, start);
    }

    for (int i = 1; i <= n; i++)
    {
        if (visit[i] == White)
            dfs_num_of_circle(i, -1);
    }
    if (sum == 0) cout << "无环！" << endl;
    else if (sum > 0)
        cout << "有环" << endl << "环的个数为：" << sum << endl;

    return 0;
}