扫描透镜
在NxM的草地上,提莫种了K个蘑菇,蘑菇爆炸的威力极大,兰博不想贸然去闯,而且蘑菇是隐形的.只 有一种叫做扫描透镜的物品可以扫描出隐形的蘑菇,于是他回了一趟战争学院,买了2个扫描透镜,一个 扫描透镜可以扫描出(3*3)方格中所有的蘑菇,然后兰博就可以清理掉一些隐形的蘑菇. 问:兰博最多可以清理多少个蘑菇?
注意:每个方格被扫描一次只能清除掉一个蘑菇。
第一行三个整数:N,M,K,(1≤N,M≤20,K≤100),N,M代表了草地的大小;
接下来K行,每行两个整数x,y(1≤x≤N,1≤y≤M).代表(x,y)处提莫种了一个蘑菇.
一个方格可以种无穷个蘑菇.
团战可以输,提莫必须死(多少年的老梗了)
这题用贪心的思想还是很简单的,就是一边遍历,一边将最大蘑菇数以及对应起点的坐标记录下来。主要是注意遍历的时候的边界条件,不要越界。
主要算法:
scan(int **board,int *result) //扫描
{
Scan_All(mushroom_in_board)
{
remember(x,y);
for i from x to x+3
for j from y to y+3
if(have_mushroom) sum++;
result[0] <- sum;
result[1] <- x;
result[2] <- y;
}
compare_max(result[0]);
x <- max_x;
y <- max_y;
}
void pick () //去除蘑菇
{
scan (board,first_scan);
pick_max(mushroom_in_board);
scan(board,second_scan);
}
具体实现:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int first_scan[3];
int second_scan[3];
void scan(vector<vector<int>>& board, int result[])
{
for (int i = 0; i < board.size() - 2; i++)
for (int j = 0; j < board[0].size() - 2; j++)
{
int sum = 0;
for (int x = i; x < i + 3; x++)
for (int y = j; y < j + 3; y++)
if (board[x][y] > 0) ++sum;
if (result[0] < sum)
{
result[0] = sum; //记录扫描蘑菇最多的起点
result[1] = i;
result[2] = j;
}
}
}
int main()
{
int n, m, k, x, y;
cin >> n >> m >> k;
if (n < 3)n = 3;
if (m < 3)m = 3;
vector<vector<int>> board(n, vector<int>(m, 0));
while (k--)
{
cin >> x >> y;
++board[x-1][y-1];
}
scan(board, first_scan);
for (int i = first_scan[1]; i < first_scan[1] + 3; i++)
for (int j = first_scan[2]; j < first_scan[2] + 3; j++)
if (board[i][j] > 0) --board[i][j];
scan(board, second_scan);
cout << first_scan[0] + second_scan[0] << endl;
return 0;
}
这个题目还是比较简单的,不过用贪心算法是得不到最优解的。我们可以举一个反例:
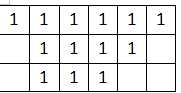
如果用贪心的思想,我们能得到如下结果
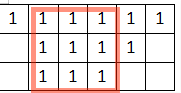
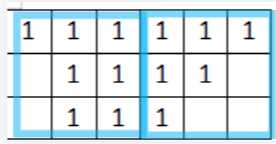
所以贪心是解决问题的一个思想,但不是最优的方法,得不到最优解。
炉石传说
GG学长虽然并不打炉石传说,但是由于题面需要他便学会了打炉石传说。但是传统的炉石传说对于刚入门的GG学长来说有点复杂,所以他决定自己开发一个简化版的炉石传说。
在简化版的炉石传说中:
每个随从只有生命值和攻击力,并且在你的回合下,你的每只随从在本回合下只能选择一个敌方随从进行攻击。当两个随从a,b交战时,a的生命值将减去b的攻击力,b的生命值将减去a的攻击力,(两个伤害没有先后顺序,同时结算)。如果a或b的生命值不大于0,该随从将死亡。
某一次对局中,GG学长和对手场面上均有n个随从,并且是GG学长的回合。由于GG学长是个固执的boy,他一定要在本回合杀死对方所有随从,并且保证自己的随从全部存活。他想知道能否做到。
第一行为T,表示有T组数据。T<=100。
每组数据第一行为n,表示随从数量(1 <= n <= 100)
接下来一行 2n 个数字a_1, b_1, a_2, b_2, … , a_n, b_n (1 <= ai, bi <= 100)
表示GG学长的n个随从,a_i 表示随从生命,b_i 表示随从攻击力
接下来一行 2n 个数字c_1, d_1, c_2, d_2, … , c_n, d_n (1 <= c_i, d_i <= 100)
表示对手的n个随从,c_i 表示随从生命,d_i 表示随从攻击力。
有一说一,这个题目用纯贪心的话。。。真不一定能写出来。题目里面无时无刻都在透露出生活哲学的气息。没错,就是那个生活哲学,绿帽算法————匈牙利算法。
匈牙利算法是一种解决二分图最大匹配的算法,什么是二分图的最大匹配。。。自行离散数学
有了匈牙利算法,事情就变得简单了。废话不多说,直接上代码:
主要算法:
bool Hungary(int x) //匈牙利算法
{
for i from 0 to n
{
if (!use(card[i]) && judge(a[i], b[i])) //如果这张牌没有使用,且使用之后可以赢,就使用它
{
use(card[i]) <- true;
if (!match[i] || Hungary(match[i])) //如果没匹配或匹配的对象有匹配,则换匹配
{
match[i] = x;
return true;
}
}
}
return false;
}
具体实现:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
typedef struct Game
{
int live, attack;
}Game;
Game a[N], b[N];
int u[N], f[N];
int judge(Game a, Game b) //判断这把是否能赢
{
if (a.attack > b.live && a.live > b.attack)
return 1;
return 0;
}
int Hungary(int x) //匈牙利算法
{
for (int i = 1; i <= n; i++)
{
if (!u[i] && judge(a[i], b[i])) //如果这张牌没有使用,且使用之后可以赢,就使用它
{
u[i] = 1;
if (!f[i] || Hungary(f[i]))
{
f[i] = x;
return 1;
}
}
}
return 0;
}
int main()
{
int T, sum;
cin >> T;
while (T--)
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i].live >> a[i].attack;
for (int i = 1; i <= n; i++)
cin >> b[i].live >> b[i].attack;
sum = 0;
for (int i = 1; i <= n; i++)
{
memset(u,0,sizeof(u));
if (Hungary(i))
sum++;
}
if (sum == n) cout << "Yes" << endl;
else cout << "No" << endl;
}
return 0;
}
(其实题目已经给了提示,主人公名字GG(Graph-Graph),这波直接二分图)
最大生成树
这个没什么好说的了,就是将Kruskal算法里面的从小到大排序改为从大到小排序就行了。
主要算法:
find(int x) // 并查集核心操作
{
if (p[x] != x)
p[x] <- find(p[x]);
return p[x];
}
kruskal()
{
sort_fromMaxtoMin(edges, edges + m);
for i from 0 to n-1
p[i] <- i; // 初始化并查集
for i from 0 to m-1
{
a <- edges[i].a, b <- edges[i].b, w <- edges[i].w;
pa <- find(a), pb <- find(b);
if (pa != pb) // 如果两个连通块不连通,则将这两个连通块合并
{
p[pa] <- pb;
add_path_length();
store_Maxtree();
}
}
if (cnt < n - 1)
None_Answer();
else
print_Maxtree();
print_MAXlength();
}
具体实现:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100010;
int n, m;
int p[N]; //并查集数组
typedef struct Graph //只要存储边就行
{
int from;
int to;
int weight;
bool operator < (const Graph& G)const
{
return G.weight < weight;
} //方便排序
}Graph;
Graph g[N]; //原图的边
Graph K[N]; //最大生成树的边
int find(int x) //并查集模板
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n >> m;
for (int i = 0; i < m; i++)
cin >> g[i].from >> g[i].to >> g[i].weight;
sort(g, g + m);
for (int i = 0; i < n; i++)p[i] = i;
int res = 0, cnt = 0;
for (int i = 0; i < m; i++)
{
int a = g[i].from; int b = g[i].to; int w = g[i].weight;
int pa = find(a); int pb = find(b);
if (pa != pb)
{
p[pa] = pb;
res += w;
K[cnt].from = a;
K[cnt].to = b;
K[cnt].weight = w;
cnt++;
}
}
if (cnt < n - 1) cout << "无最大生成树" << endl;
else
{
cout << "最大生成树为:" << endl;
for (int i = 0; i < cnt; i++)
{
cout << K[i].from << "-----" << K[i].to << endl;
}
cout << "路径长度为" << endl;
cout << res << endl;
}
return 0;
}



0 条评论