八数码问题

八数码问题

在一个 3×3 的网格中，1∼8 这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。

例如：

1 2 3
x 4 6
7 5 8

在游戏过程中，可以把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1 2 3
4 5 6
7 8 x

例如，示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1 2 3　　1 2 3　　1 2 3　　1 2 3
x 4 6　　4 x 6　　4 5 6　　4 5 6
7 5 8　　7 5 8　　7 x 8　　7 8 x

现在，给你一个初始网格，请你求出得到正确排列至少需要进行多少次交换。

最早接触八数码问题是人工智能的实验，给了源码让我们改算法参数（笑死，根本不知道怎么改）
当时给了好几种算法，这里介绍一下BFS算法实现八数码问题。
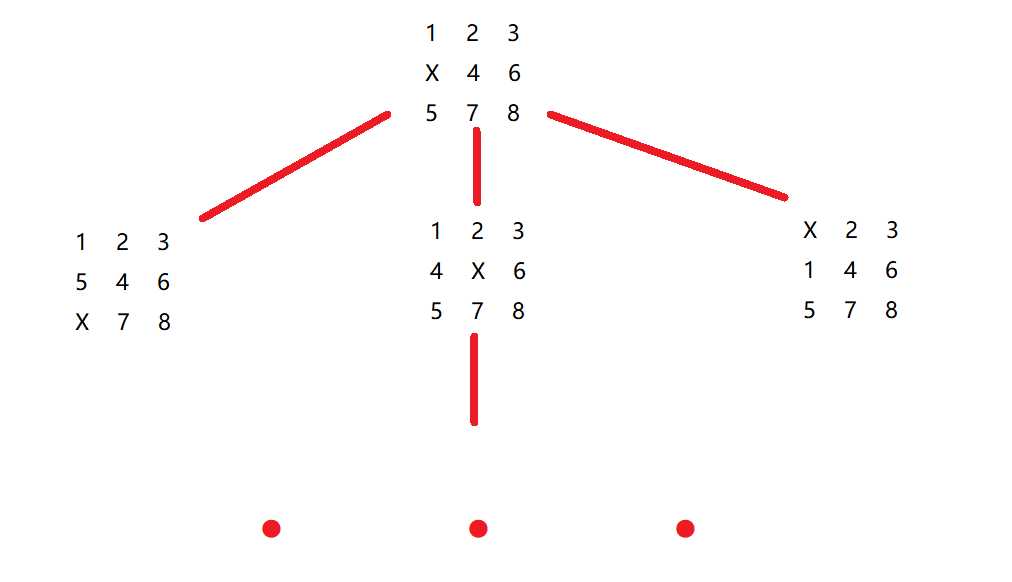
事实上，就是将‘x’附近的数字进行移动，将每一步的过程以类似于树的状态广度遍历，也可以简单理解为遍历所有可能性，看最早到达目的状态的步数是多少。

• 具体实现：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#include <unordered_map>

using namespace std;

int BFS(string start)
{
    string end = "12345678x";
    queue <string> q;                   //状态队列
    unordered_map <string, int> dis;    //距离数组

    q.push(start);
    dis[start] = 0;
    int dx[4] = { -1,0,1,0 };
    int dy[4] = { 0,1,0,-1 };

    while (q.size())
    {
        auto t = q.front();      //记录队列头部
        q.pop();
        int distance = dis[t];
        if (t == end) return distance;         //达到目标状态，返回距离

        int k = t.find('x');    //找到x的坐标
        int x = k / 3, y = k % 3;    //将对应的一维坐标改为二维坐标

        for (int i = 0; i < 4; i++)
        {
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < 3 && b >= 0 && b < 3)  //没有越界
            {
                swap(t[k], t[a * 3 + b]);          //将与x相邻的方块进行移位
                if (!dis[t])                       //如果t状态的距离没有改变过
                {
                    dis[t] = distance + 1;
                    q.push(t);                    //状态存入队列
                }
                swap(t[k], t[a * 3 + b]);         //恢复现场
            }
        }
    }
    return -1;

}


int main()
{
    string start;
    for (int i = 0; i < 9; i++)
    {
        char c;
        cin >> c;
        start += c;
    }
    int ans = BFS(start);
    if (ans != -1)
        cout << "转换步数：" << ans << endl;
    else cout << "无法转换！" << endl;

    return 0;
}