01.两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9
-10^9 <= target <= 10^9
只会存在一个有效答案
AC Code
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> heap;
for (int i=0; i<nums.size(); i++)
{
int r=target-nums[i];
if(heap.count(r)) return {heap[r],i};
heap[nums[i]]=i;
}
return {};
}
};
02.两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。

示例 1:
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
提示:
每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9
题目数据保证列表表示的数字不含前导零
AC Code
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
auto dummy=new ListNode(-1),cur=dummy; //虚拟头节点,尾节点
int t=0; //进位
while(l1||l2||t)
{
if (l1) t+=l1->val,l1=l1->next;
if (l2) t+=l2->val,l2=l2->next;
cur=cur->next=new ListNode(t%10);
t/=10;
}
return dummy->next;
}
};
03.无重复的最长字子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,”pwke” 是一个子序列,不是子串。
示例 4:
输入: s = ""
输出: 0
提示:
0 <= s.length <= 5 * 10^4
s 由英文字母、数字、符号和空格组成
题意分析
以字符串的最后一个字母的位置进行分类,即可分为 n 类
AC Code
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<char,int> heap;
int res=0;
for (int i=0,j=0; i<s.size(); i++)
{
heap[s[i]]++;
while(heap[s[i]]>1) heap[s[j++]]--;
res=max(res,i-j+1);
}
return res;
}
};
04. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
示例 3:
输入:nums1 = [0,0], nums2 = [0,0]
输出:0.00000
示例 4:
输入:nums1 = [], nums2 = [1]
输出:1.00000
示例 5:
输入:nums1 = [2], nums2 = []
输出:2.00000
提示:
nums1.length = m
nums2.length = n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-10^6 <= nums1[i], nums2[i] <= 10^6
进阶:你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗
题意分析
找到两个数组中第 k 个数
A[k/2]<B[k/2] ,则 A 中的前 k/2 位数就可以被删除
B[k/2]<A[k/2] ,则 B 中的前 k/2 位数就可以被删除
A[K/2]=B[k/2] ,则 A[k/2]=B[k/2]=kth\ \ element
$O(log(m+n))$
AC Code
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size(),m = nums2.size(),sum = n + m;
if(sum % 2 == 0)
{
int left = getKthSmallest(nums1,0,nums2,0,sum / 2);
int right = getKthSmallest(nums1,0,nums2,0,sum / 2 + 1);
return (left + right) / 2.0;
}else
return getKthSmallest(nums1,0,nums2,0,sum / 2 + 1);
}
int getKthSmallest(vector<int> &nums1,int i,vector<int> &nums2,int j,int k)
{
if(nums1.size() - i > nums2.size() - j) return getKthSmallest(nums2,j,nums1,i,k);
if(i == nums1.size()) return nums2[j + k - 1];
if(k == 1) return min(nums1[i],nums2[j]);
int si = min(i + k / 2,(int)nums1.size()),sj = j + k / 2;
if(nums1[si - 1] > nums2[sj - 1])
return getKthSmallest(nums1,i,nums2,j + k / 2,k - k / 2);
else
return getKthSmallest(nums1,si,nums2,j,k - (si - i));
}
};
05. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
示例 3:
输入:s = "a"
输出:"a"
示例 4:
输入:s = "ac"
输出:"a"
提示:
1 <= s.length <= 1000
s 仅由数字和英文字母(大写和/或小写)组成
题意分析
- 回文串
- 长度为奇数:满足左右对称
- 长度为偶数:两两配对
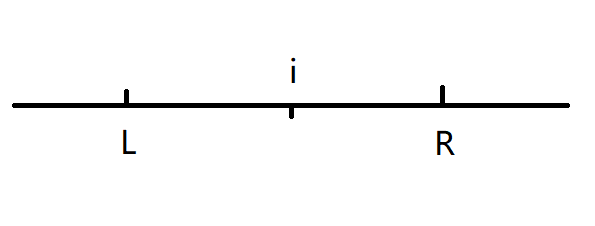
- $length=R-L-1$
- $if ((length \mod 2)=1),\ l=i-1,r=i+1$
- $if ((length\mod 2)=0),\ l=i,r=i+1$
AC Code
class Solution {
public:
string longestPalindrome(string s) {
string res;
for (int i=0; i<s.size(); i++)
{
int l=i-1,r=i+1; //枚举长度为奇数的情况
while(l>=0 && r<s.size() && s[l]==s[r]) l--,r++;
if (res.size()<r-l-1) res=s.substr(l+1,r-l-1);
l=i,r=i+1;
while(l>=0 && r<s.size() && s[l]==s[r]) l--,r++;
if (res.size()<r-l-1) res=s.substr(l+1,r-l-1);
}
return res;
}
};
06. Z 字形变换
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 “PAYPALISHIRING” 行数为 3 时,排列如下:
P A H N
A P L S I I G
Y I R
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:”PAHNAPLSIIGYIR“。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入:s = "PAYPALISHIRING", numRows = 3
输出:"PAHNAPLSIIGYIR"
示例 2:
输入:s = "PAYPALISHIRING", numRows = 4
输出:"PINALSIGYAHRPI"
解释:
P I N
A L S I G
Y A H R
P I
示例 3:
输入:s = "A", numRows = 1
输出:"A"
提示:
1 <= s.length <= 1000
s 由英文字母(小写和大写)、’,’ 和 ‘.’ 组成
1 <= numRows <= 1000
题意分析
- 首行的公差为 2n-2
- 每一行的公差都是 2n-2 ,但是在输出时要跨项输出
- 斜线上的起始点的计算为:起始点所对应的数 i 和其对应行的第一个数的和为 2n-2 ,第二个数为 2n-2-i
AC Code
class Solution {
public:
string convert(string s, int numRows) {
string res;
if (numRows==1) return s;
for (int i=0; i<numRows; i++)
{
if(i==0 || i==numRows-1)
{
for (int j=i; j<s.size(); j+=2*numRows-2)
res+=s[j];
}
else
{
for (int j=i,k=2*numRows-2-i; j<s.size() || k<s.size(); j+=2*numRows-2,k+=2*numRows-2)
{
if (j<s.size()) res+=s[j];
if (k<s.size()) res+=s[k];
}
}
}
return res;
}
};
07. 整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−2^{31}, 2^{31} − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入:x = 123
输出:321
示例 2:
输入:x = -123
输出:-321
示例 3:
输入:x = 120
输出:21
示例 4:
输入:x = 0
输出:0
提示:
-2^{31} <= x <= 2^{31} – 1
AC Code
class Solution {
public:
int reverse(int x) {
long long r=0;
while(x)
{
r=r*10+x%10;
x/=10;
}
if (r>INT_MAX) return 0;
if (r<INT_MIN) return 0;
return r;
}
};
08. 字符串转换整数 (atoi)
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
读入字符串并丢弃无用的前导空格
检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数(即,”123″ -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。
如果整数数超过 32 位有符号整数范围 [−2^{31}, 2^{31} − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −2^{31} 的整数应该被固定为 −2^{31} ,大于 2^{31} − 1 的整数应该被固定为 2^{31} − 1 。
返回整数作为最终结果。
注意:
本题中的空白字符只包括空格字符 ‘ ‘ 。
除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
示例 1:
输入:s = "42"
输出:42
解释:加粗的字符串为已经读入的字符,插入符号是当前读取的字符。
第 1 步:"42"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"42"(当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"42"(读入 "42")
^
解析得到整数 42 。
由于 “42” 在范围 [-2^{31}, 2^{31} – 1] 内,最终结果为 42 。
示例 2:
输入:s = " -42"
输出:-42
解释:
第 1 步:" -42"(读入前导空格,但忽视掉)
^
第 2 步:" -42"(读入 '-' 字符,所以结果应该是负数)
^
第 3 步:" -42"(读入 "42")
^
解析得到整数 -42 。
由于 “-42” 在范围 [-2^{31}, 2^{31} – 1] 内,最终结果为 -42 。
示例 3:
输入:s = "4193 with words"
输出:4193
解释:
第 1 步:"4193 with words"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"4193 with words"(当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"4193 with words"(读入 "4193";由于下一个字符不是一个数字,所以读入停止)
^
解析得到整数 4193 。
由于 “4193” 在范围 [-2^{31}, 2^{31} – 1] 内,最终结果为 4193 。
示例 4:
输入:s = "words and 987"
输出:0
解释:
第 1 步:"words and 987"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"words and 987"(当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"words and 987"(由于当前字符 'w' 不是一个数字,所以读入停止)
^
解析得到整数 0 ,因为没有读入任何数字。
由于 0 在范围 [-2^{31}, 2^{31} – 1] 内,最终结果为 0 。
示例 5:
输入:s = "-91283472332"
输出:-2147483648
解释:
第 1 步:"-91283472332"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"-91283472332"(读入 '-' 字符,所以结果应该是负数)
^
第 3 步:"-91283472332"(读入 "91283472332")
^
解析得到整数 -91283472332 。
由于 -91283472332 小于范围 [-2^{31}, 2^{31} – 1] 的下界,最终结果被截断为 -2^{31} = -2147483648 。
提示:
0 <= s.length <= 200
s 由英文字母(大写和小写)、数字(0-9)、’ ‘、’+’、’-‘ 和 ‘.’ 组成
AC Code
class Solution {
public:
int myAtoi(string s) {
int k=0;
while(k<s.size() && s[k]==' ') k++; //过滤空白字符
if (k==s.size()) return 0;
int flag=1; //默认符号为正
if (s[k]=='-') flag=-1,k++;
else if (s[k]=='+') k++;
long long res=0;
while(k<s.size() && s[k]>='0' && s[k]<='9')
{
res=res*10+s[k]-'0';
k++;
if (res>INT_MAX) break;
}
res*=flag;
if (res>INT_MAX) res=INT_MAX;
else if (res<INT_MIN) res=INT_MIN;
return res;
}
};
09. 回文数
给你一个整数 x,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。例如,121 是回文,而 123 不是。
示例 1:
输入:x = 121
输出:true
示例 2:
输入:x = -121
输出:false
解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10
输出:false
解释:从右向左读, 为 01 。因此它不是一个回文数。
示例 4:
输入:x = -101
输出:false
提示:
-2^{31} <= x <= 2^{31} – 1
AC Code
class Solution {
public:
bool isPalindrome(int x) {
// if (x<0) return 0;
// else
// {
// string s=to_string (x);
// return s==string(s.rbegin(),s.rend());
// } //转换为字符串再倒置判断
if (x<0) return 0;
long long res=0,x1=x;
while(x)
{
res=res*10+x%10;
x/=10;
}
return res==x1;
}
};
010. 正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s 的,而不是部分字符串。
示例 1:
输入:s = "aa" p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa" p = "a*"
输出:true
解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab" p = ".*"
输出:true
解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:s = "aab" p = "c*a*b"
输出:true
解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:s = "mississippi" p = "mis*is*p*."
输出:false
提示:
0 <= s.length <= 20
0 <= p.length <= 30
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
保证每次出现字符 * 时,前面都匹配到有效的字符
题意分析

AC Code
class Solution {
public:
bool isMatch(string s, string p) {
int n=s.size(),m=p.size();
s=' '+s,p=' '+p;
vector<vector<bool>> f(n+1,vector<bool>(m+1));
f[0][0]=true;
for (int i=0; i<=n; i++)
for (int j=1; j<=m; j++)
{
if (j+1<=m && p[j+1]=='*') continue;
if (i&&p[j]!='*') f[i][j]=f[i-1][j-1] && (s[i]==p[j] || p[j]=='.');
else if(p[j]=='*')
{
f[i][j]=f[i][j-2] || i&&f[i-1][j] && (s[i]==p[j-1] || p[j-1]=='.');
}
}
return f[n][m];
}
};


0 条评论