TARE 论文笔记

TARE RSS

0.论文链接

• TARE: A Hierarchical Framework for Efficiently Exploring Complex 3D Environments

1. 论文背景

• 本文主要是提出一种机器人运动路径的自我探索方法
• 如何优化了整体探索路径与路径长度的关系，得到运动学可行局部路径

2. 研究思路

​ 利用全局表示来规划路径，对于规划的路径进行详细的探索，将局部最优路径和全局路径两层路径重叠组合来确定，追求整体最优解而非即时奖励的最大化。利用递归和随机取样——最小视点集。

​ 将空间分为自由空间和非自由空间，非自由空间分为自占据空间和未知空间。在线实时更新未覆盖面，在给定的未覆盖面和当前视点来看找一系列的视点来满足条件。

​ 算法概念如下：

• 先进行视点采样进行选点，并将所选的点进行迭代。
• 迭代式预选三个视点来进行局部最短路径的探索，并将局部与全局路径连接 —— （分步思想）
• 奖励与概率成正比，当奖励可以忽略时，采样结束，找到局部成本最低的路径
• 考虑到机器人的运动学和动力学需求，要改进平滑路径
• 利用 TSP 来分段和重整平滑段，只对相邻点的样条进行优化
• 用 T_{local} 代替 T_{global} 。

3. 实验结果

• 实验优化的结果显著

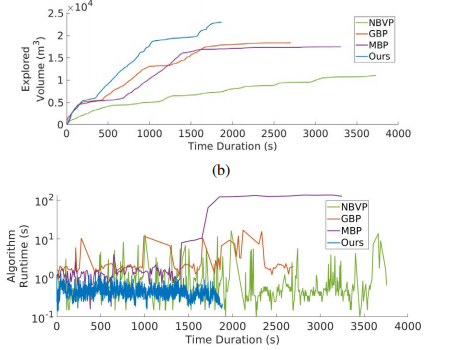
4. 创新点和不足

• 创新点：
  • 在探索的过程中，选取视点进行分段处理，将一个整体的最优路径改为一段段的局部路径之和，并且在每一段的连接过程中考虑运动学特性，并且不断迭代和优化
  • 在探索的过程中采用贪心的思想，每次只看一个视点，减少了时间复杂度
• 不足：
  • 采用 TSP 思想选取视点，在解决 TSP 问题上的算法的运算占最大的比重
  • 迭代预选的三个点是随机选取的，对于迭代时间复杂度的影响较大

5. 个人想法

• 在路径规划时的分段思想和迭代优化思想值得借鉴
• 贪心思想来减小复杂度的思想可以借鉴

会后补充

• 一边维护，一边优化
• 分层化
• 局部优化还需要考虑